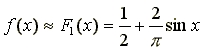Fourierpolynom

Fourier, Josef (1768-1830;62)	Während Taylorpolynome und Taylorreihe dazu geeignet sind, Funktionen lokal zu approximieren, nämlich in ihrem Entwicklungszentrum, versagt das Verfahren bei globaler Approximation. Für eine globale Approximation eignen trigonometrische Funktionen besser. Das führt uns zu den Fourierreihen. In einem weiteren Punkt unterscheiden sich Fourier- von Taylorapproximationen. Fourierapproximationen sind periodisch, sie eignen sich also besonders für periodische Funktionen. Der einfachheitshalber beschränken wir uns zunächst auf 2-p-periodische Funktionen. Diese Beschränkung lassen wir später wieder fallen. Wir versuchen ein 2-p-periodische Funktion durch folgende Form zu approximieren.
Fourier- koeffizienten	Die Funktion F_n ist also Fourierpolynom vom Grade n bekannt. Die Koeefizienten a_k und b_k werden als Fourierkoeffizienten bezeichnet. Da alle Funktionen cos(kx) und sin(kx) 2-p-periodisch sind, ist auch F_n 2-p-periodisch, also das ist schon einmal günstig für unsere Annahme. Um nun tatsächlich F_n zu finden brauchen wir "nur noch die Fourierkoeefizienten geeignet zu bestimmen". 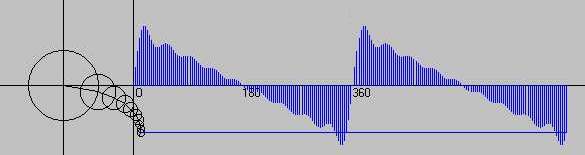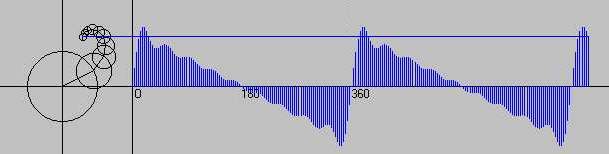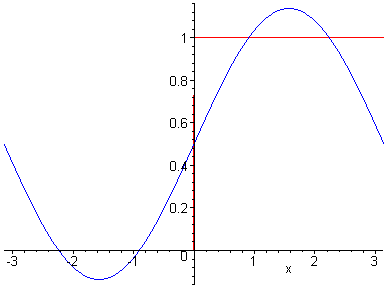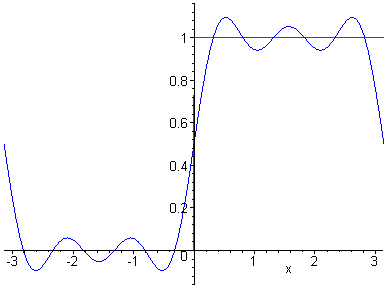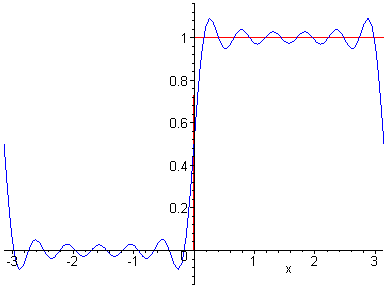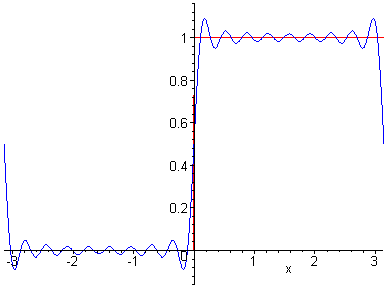Wir wählen sie, wie folgt Man beachte dabei, dass a₀ der Durchschnittswert der Funktion f im Intervall [-p,p] ist. (Zum Beweis) Die Funktionen F_n kann man sich als Projektionen von Epizykeln vorstellen. Ein Punkt wandert auf einem Kreis, dessen Mittelpunkt selbst auf einem Kreis wandert usw. Von Kreis zu Kreis erhöht sich die Frequenz (kte-Kreis k-fache Grundfrequenz, wir interpretieren dabei x als Zeit und k als ganzzahliges Vielfache der Grundfrequenz w = 1s^-1), die Radien entsprechen den Fourierkoeffizienten. Siehe dazu die nachfolgenden beiden Abbildungen. Es läßt sich schon erahnen, welche Funktion approximiert werden soll. Wir wollen ein einfaches Beispiel durchrechnen. Für kompliziertere Beispiele verwenden wir dann das CAS-Programm Maple V.
Beispiel	Es soll die Funktion f mit durch F₁ und F₃ approximiert werden. Wir denken uns dazu die Funktion auf R periodisch fortgesetzt, um dann F₁ bzw. F₃ wieder auf das Intervall [-p,p] zu beschränken. Wir berechnen die die Fourrierkoeefizienten a₀, a₁ und b₁: und weiter und schließlich Damit haben wir das Fourierpolynom 1ten Grades für f gefunden: Um das Fourierpolynom 3ten Grades zu bestimmen, müssen wir lediglich noch a₂, a₃, b₂ und b₃ bestimmen. Die Erhöhung des Grades des Fourierpolynoms von 1 auf 2 bringt für F₂ gegenüber F₁ keine Veränderung. Für das Fourierpolynom 3ten Grades erhalten wir demnach: Entsprechende Berechnungen liefern F₅ und F₇
Animation Maple-Prozedur Download des Maple V - Worksheets	Mit Hilfe einer Maple-Prozedur, können wir Fourier-Polynom-Animation zu erstellen. Die Periodenlänge wird dabei durch geeignete Transformation und Abänderung der Formeln zur Bestimmung der Fourierkoeefizienten variabel gehalten. Siehe dazu mehr unter "beliebige Periodenlänge". Für unsere oben diskutierte Funktion haben wir folgende Animation: Maple berechnet die Folge der F₁ bis F₁₇, erstellt die Graphen und legt sie nacheinander auf den Bildschirm, dass der Animationeffekt entsteht.
weitere Beispiele	Bei den Beispielen handelt es sich um nicht-periodische Funktionen. Dazu beschränken wir die Funktion auf ein endliches Intervall und setzt sie dann auf ganz R wieder periodisch fort. Das gewonnene Fourierpolynom schränkt man dann wieder auf das Original-Intervall ein. Dass es dabei an den Rändern Probleme gibt, ist offensichtlich und kann man bei den Animationen leicht erkennen. im Bereich [0,10] bis F₂₀ im Bereich [-2,3] bis F₁₅ im Bereich [-3,3] bis F₁₅ im Bereich [-2,2] bis F₁₅ Denkt man sich die Funktionen periodiosch fortgesetzt, so zeigen einige an den Nahstellen Unstetigkeit. Genau an diesen Unstetigkeitsstellen aber erkennt man, dass auch durch weitere Erhöhung des Approximationsgrades die Funktionen nicht besser angenähert werden können.
(c) Pohlig