31.3 Heapsort
31.3.1 Die Idee
 
Was ist ein Heap? Der Heapsortalgorithmus lässt sich am besten an einem Binärbaum (vgl. dazu Kap. 28.11) erklären. Hilfreich beim Verständnis ist eine Eigenschaft eines Baumes, die wir 'heap' nennen wollen. Diese Eigenschaft ist an die sog. Heapbedingung geknüpft.  Wir erklären zunächst für einen Elementarbaum, der nur aus einem Vater- und einem bzw. zwei Söhneknoten besteht: Einen solchen Elementarbaum nenn wir 'heap', wenn der Wert des Vaterkotens kleiner ist, als die Werte der Söhneknoten.
Wir dehnen nun die Eigenschaft aus und nenn einen Baum im Knoten i dann heap, wenn die Söhne des Knotens nicht größere Werte haben und jeder Teilbaum ab dem Knoten i abwärts selbst wieder heap ist. Die Rekursion endet in den Blättern eines Baumes, sie verweisen auf einen leeren Baum, für den Heap-Bedingung a priori erfüllt ist.

Diese rekursive Definition veranschaulichen wir uns an einem einfachen Beispiel (siehe unten).
Wir beginnen bei den Blättern, es sind dies die Knoten  . Sie sind, wie gesagt, a priori heap. Nun sind die Teilbäume in Knoten K-3, K- 4 und K-5 heap, weil deren Söhne nicht kleinere Werte haben. Der Teilbaum im Knoten K-2 ist heap, da seine Söhne, die Knoten K-4 und K- 5 keine kleinere Werte haben; und schließlich sind alle seine Teilbäume, wie schon nachgewiesen ebenfalls heap.
 
Heap-Bedingung

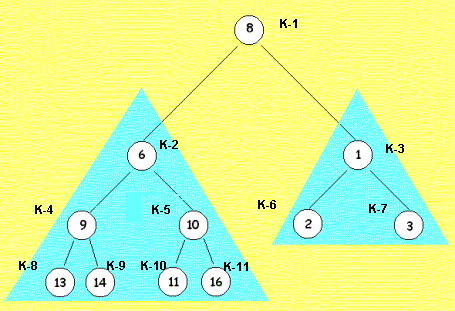
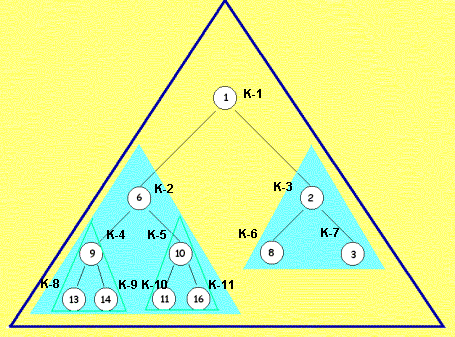
Im ersten Knoten, der Wurzel des Gesamtbaums mit dem Wert 8, ist der Baum nicht heap, da seine Söhne, es sind die Knoten K-2 und K-3, kleinere Werte haben. Der Gesamtbaum erfüllt also die Heapbedingung nicht. Wir beschreiben nun einen Weg, der einen beliebigen Binärbaum vollständig heap macht.
 
Ein Baum wird heap In unserem Beispiel gehen von einem Baum aus, der teilweise schon heap ist, und zwar in den Knoten K-3,K- 4, K-5, K-6, K-7, K-8, K-9, K-10 und K- 11. Diese Knoten sind entweder Väter von Knoten deren Werte nicht kleiner sind, oder es handelt sich um Blätter.

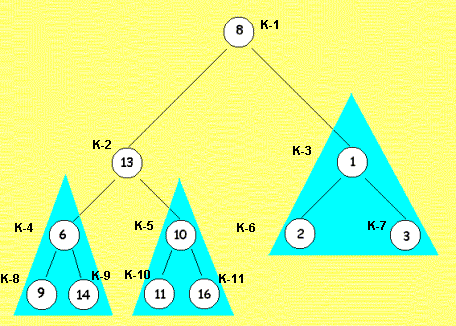
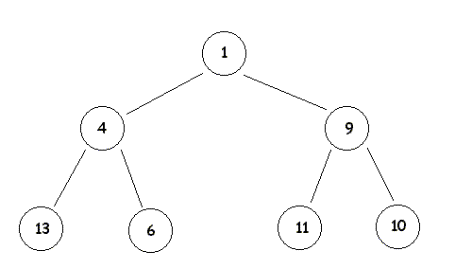
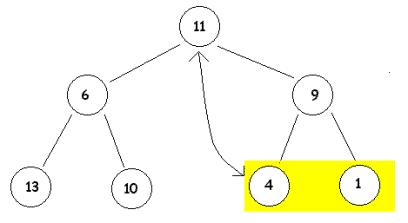
Auf unseren Weg zum Baum, der schon von der Wurzel her heap ist, versuchen wir zunächst, den Konten mit der kleinsten Nummer, der noch nicht heap ist, heap zu machen: Also muss Knoten K-2 mit dem Wert 13 und sein Sohn, also
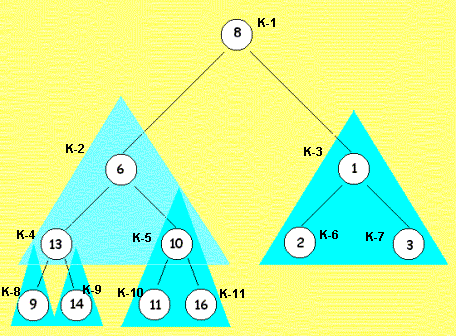
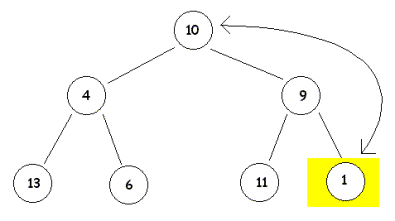
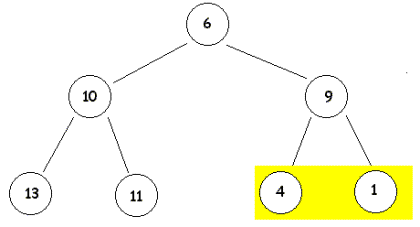
K-4 ihre Werte tauschen. Wir erhalten:
 
 

Jetzt hat zwar Knoten K-2 mit dem Wert 6 nur Söhne mit nicht kleineren Werten, aber nicht mehr alle Unterbäume sind heap. Knoten 4 mit dem Wert 13 ist Wurzel eines Elementarbaumes der nicht mehr heap ist. Wir müssen also bei den Söhnen nachschauen, ob sie ihre heap-Bedingng verloren haben und müssen u.U. nachbessern. Wir erreichen das, indem wir Knoten K-4 und Knoten K-8 ihre Werte tauschen lassen.
 

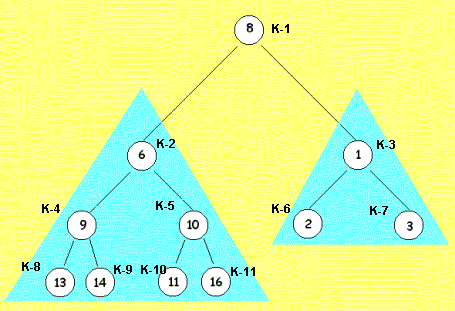
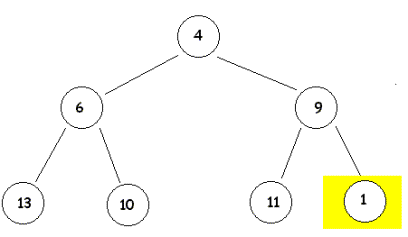
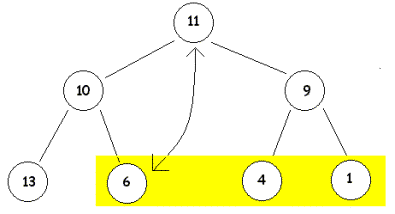
Wie die Darstellung des Baums zeigt, sind wir unserem Ziel, den gesamten Baum heap zu machen ein Stück näher gekommen. Knoten 1 muss mit Konten K-3 die Werte 8 und 1 austauschen, danach die Konten K-3 und K-6 die Werte 8 und 2 und der gesamte Baum ist heap.
 

 
Mit heapen Bäumen sortieren Wie man leicht nachvollziehen kann, wird beim Heap-Machen eines binären Baumes das kleinste Element zur Wurzel hochgespült. Diese Tatsache nützt man zum sog. Heap-Sortieren, oder kurz HeapSort.

Wir geben einen Baum vor, der vollkommen heap ist.

 
  Die Wurzel und der letzte Knoten (Nummer 7) tauschen ihre Werte. Der letzte Knoten wird "eingefroren" und 'gehört' somit nicht mehr zum Baum.

Der Restbaum wird wieder heap gemacht. Die im Restbaum kleinste Zahl hat es danach in die Wurzel "gespült".

Wurzel und der letzte Knoten des verbliebenen Baumes (Nummer 6) tauschen ihre Werte, Platz 6 wird eingefroren.

Wieder wird der neue Restbaum heap gemacht.

Wurzel und letzter Knoten (Nummer 5) tauschen ihre Werte und Platz 5 wird eingefroren.

Als kleine Übung spiele man das Spiel zu Ende. Gelb unterlegt erscheint die sortierte Liste. Allerdings, ist die Liste abfallend sortiert. Man überlege sich, wie man mit dem Heapsort-Alögorithmus die Liste aufsteigend sortiert
 
zu 31.3.2 Implementierung
zur Startseite www.pohlig.de  (C) MPohlig 2004