32 Aufwand und O-Kalkül
32.1 Sortieraufwand experimentell
One plus one is two.
Two plus two is four
Four plus four is eight.
Eight plus eight is more than ten.
Kinderreim
|
|
Ein einfaches Programm (siehe
Download) testet den zeitlichen Aufwand, den die einzelnen
Sortieralgoritmen benötigen: |
|
Download:
Sortieren Vergleich.java
Sortieren.java
StoppUhr.java |
public class SortierenVergleich {
public static void main(String[] args){
StoppUhr uhr = new StoppUhr();
int[] liste1;
System.out.print("Laenge der Liste: ");
int anzahl = Console.in.readInt();
liste1 = Sortieren.listeAnlegen(anzahl);
int[] liste2 = (int[]) liste1.clone();
int[] liste3 = (int[]) liste1.clone();
int[] liste4 = (int[]) liste1.clone();
uhr.starten();
Sortieren.bubbleSort(liste1);
uhr.stoppen();
System.out.println("\n\nSortierzeit BubleSort: "+uhr);
uhr.starten();
Sortieren.einfuegen(liste2);
uhr.stoppen();
System.out.println("\n\nSortierzeit Einfuegen: "+uhr);
uhr.starten();
Sortieren.heapSort(liste3);
uhr.stoppen();
System.out.println("\n\nSortierzeit HeapSort: "+uhr);
uhr.starten();
Sortieren.quickSort(liste4);
uhr.stoppen();
System.out.println("\n\nSortierzeit QuickSort: "+uhr);
}
}
|
| |
Um sicherzustellen, dass immer die
gleiche Liste von Zufallszahlen sortiert wird, erzeugen wir einmal eine
Liste liste1
und durch Klonen erzeugen wir die Instanzen
liste2,
liste3
und liste4. |
| |
Deutliche Unterschiede in der
benötigten Sortierzeit zeigen sich mit steigender Anzahl der zu
sortierenden Zahlen in den Listen. Die Stärken von Quicksort und Heapsort
zeigen sich am deutlichsten bei sehr großen Listen. Um eine Statistik zu
machen dient ein anderes kleines Programm:
|
Download:
SortierVergleich2. java |
public class SortierenVergleich2 {
public static void main(String[] args){
StoppUhr uhr = new StoppUhr();
int stat = 10;
for(int i = 5000; i < 100000; i += 5000) {
long totalZeitBubble = 0;
long totalZeitEinfuegen = 0;
long totalZeitHeap = 0;
long totalZeitQuick = 0;
for (int j = 0; j < stat; j++){
int[] liste1 = Sortieren.listeAnlegen(i);
int[] liste2 = (int[]) liste1.clone();
int[] liste3 = (int[]) liste1.clone();
int[] liste4 = (int[]) liste1.clone();
uhr.starten();
Sortieren.bubbleSort(liste1);
uhr.stoppen();
totalZeitBubble += uhr.getLaufzeit();
uhr.starten();
Sortieren.einfuegen(liste2);
uhr.stoppen();
totalZeitEinfuegen += uhr.getLaufzeit();
uhr.starten();
Sortieren.heapSort(liste3);
uhr.stoppen();
totalZeitHeap += uhr.getLaufzeit();
uhr.starten();
Sortieren.quickSort(liste4);
uhr.stoppen();
totalZeitQuick += uhr.getLaufzeit();
}
System.out.println("n = "+i);
System.out.println("--------------");
System.out.println("BubbleSort : "
+totalZeitBubble/1000.0/stat);
System.out.println("Einfuegen : "
+totalZeitEinfuegen/1000.0/stat);
System.out.println("HeapSort : "
+totalZeitHeap/1000.0/stat);
System.out.println("QuickSort : "
+totalZeitQuick/1000.0/stat);
System.out.println("\n");
}
}
}
|
| |
Um statistische Streuungen zu
minimieren, werden alle Werte 10 mal erfasst und ihr Durchschnittswert
ausgegeben. Achtung: Die Laufzeit des Programms ist selbst bei schnellen
Rechnern sehr groß: Für eine Pentium III 450 MHz und 256 MB Hauptspeicher
ergaben sich folgende Werte:
|
| |
n = 5000
--------------
BubbleSort : 0.516
Einfuegen : 0.205
HeapSort : 0.015
QuickSort : 0.0050
|
n = 10000
--------------
BubbleSort : 1.978
Einfuegen : 0.756
HeapSort : 0.015
QuickSort : 0.01 |
n = 15000
--------------
BubbleSort : 4.226
Einfuegen : 1.7425
HeapSort : 0.025
QuickSort : 0.01
|
n = 20000
--------------
BubbleSort : 7.3405
Einfuegen : 3.1245
HeapSort : 0.0305
QuickSort : 0.02 |
n = 25000
--------------
BubbleSort : 11.291
Einfuegen : 4.882
HeapSort : 0.05
QuickSort : 0.02
|
n = 30000
--------------
BubbleSort : 16.113
Einfuegen : 7.05
HeapSort : 0.055
QuickSort : 0.025 |
n = 35000
--------------
BubbleSort : 21.776
Einfuegen : 9.639
HeapSort : 0.065
QuickSort : 0.025
|
n = 40000
--------------
BubbleSort : 28.256
Einfuegen : 12.593
HeapSort : 0.085
QuickSort : 0.03 |
n = 45000
--------------
BubbleSort : 35.6565
Einfuegen : 16.003
HeapSort : 0.09
QuickSort : 0.03
|
n = 50000
--------------
BubbleSort : 46.342
Einfuegen : 20.074
HeapSort : 0.1
QuickSort : 0.04 |
n = 55000
--------------
BubbleSort : 53.9175
Einfuegen : 23.8945
HeapSort : 0.12
QuickSort : 0.04
|
n = 60000
--------------
BubbleSort : 63.0255
Einfuegen : 28.401
HeapSort : 0.13
QuickSort : 0.05 |
n = 65000
--------------
BubbleSort : 77.316
Einfuegen : 33.624
HeapSort : 0.135
QuickSort : 0.055
|
n = 70000
--------------
BubbleSort : 88.963
Einfuegen : 39.051
HeapSort : 0.1555
QuickSort : 0.05 |
n = 75000
--------------
BubbleSort : 103.3435
Einfuegen : 45.32
HeapSort : 0.1705
QuickSort : 0.06 |
|
| |
|
|
|
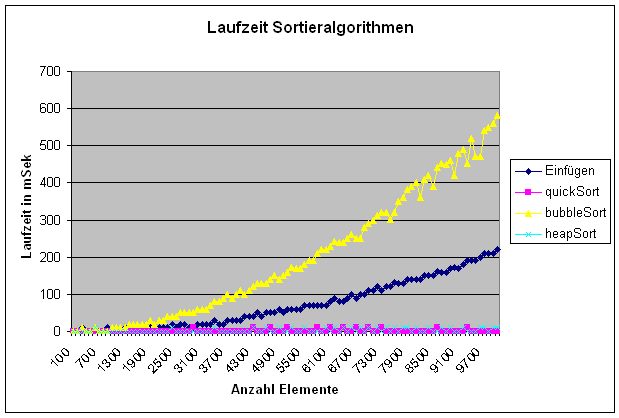
Grafische Darstellung (AMD
1,4 GHz, 512 MB DDR RAM; Einzelwertmessungen
ohne MIttelwertbildung):
 |
| |
|
|
zu |
32.2 Definition des O-Kalküls |
|
zur Startseite |
www.pohlig.de (C)
MPohlig 2004 |
