|
11.2 Beispiele (if-else) |
|
| if-else |
Die Syntax einer Verzweigung in Java
hat folgende Gestalt:
if(<Bedingung>){ Dabei kann <Bedingung> direkt ein
boolscher Wert (true oder false) sein oder aber ein Ausdruck, der zu einem
boolschen Ausdruck ausgewertet wird.
|
| Beispiel 1 |
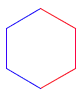 Wir stellen uns
vor, dass eine Turlte das links dargestellte Bild erzeugt und zwar auf
folgendem Wege. Sie startet am unteren linken unteren (Süd-West) Punkt und
zeichnet bei jedem Klick auf den zeichne!-Schalter eine weitere Seite des
Sechsecks. Die Farbe soll dann automatisch umspringen. Wenn man ein
mal die Richtungen der Turtle anschaut, und wenn man weiß, dass der
Orientierungswinkel der Turtle als Winkel zur einer gedachten Rechtsachse
im mathematisch positiven Sinne gemessen wird, ist es nicht sehr schwer zu
erkenne, dass die Spur der Turtle rot gefärbt wird, wenn dieser Winkel
größer also 1800 misst. Wir stellen uns
vor, dass eine Turlte das links dargestellte Bild erzeugt und zwar auf
folgendem Wege. Sie startet am unteren linken unteren (Süd-West) Punkt und
zeichnet bei jedem Klick auf den zeichne!-Schalter eine weitere Seite des
Sechsecks. Die Farbe soll dann automatisch umspringen. Wenn man ein
mal die Richtungen der Turtle anschaut, und wenn man weiß, dass der
Orientierungswinkel der Turtle als Winkel zur einer gedachten Rechtsachse
im mathematisch positiven Sinne gemessen wird, ist es nicht sehr schwer zu
erkenne, dass die Spur der Turtle rot gefärbt wird, wenn dieser Winkel
größer also 1800 misst. |
|
Download: Verzweigung.java |
|
| Passiert oft, ist aber für Anfänger nicht zu empfehlen |
Wenn der Anweisungsblock, wie in
unserem Beispiel aus nur einer Anweisung besteht, kann man die
Blockklammern weglassen.
|
| Das Einrücken ist dringend zu empfehlen, um auch optisch deutlich zu machen, was zu einem Verzweigungsblock gehört und was nicht. | |
|
Beispiel 2 das Ulam-Spiel |
Das Ulam-Spiel hat folgende
Spielregeln: Wählen Sie eine Zahl und führen Sie den folgenden Algorithmus durch: Wiederhole Nehmen wir als Startwert 3, so ergibt sich folgende Folge: 3 - 10 - 5 - 16 - 8 - 4 - 2 - 1 - 4 - 2 - 1 - 4 - 2 - 1.... Eigentlich können wir bei 1 aufhören, da sich danach die Zahlen 4 - 2 - 1 immer wieder wiederholen. Für die Startzahl 23 erhalten wir die Zahlenfolge: 23 - 70 - 35 - 106 - 53 - 160 - 80 - 40 - 20 - 10 - 5 - 16 - 8 - 4 - 2 - 1 Das eigenartige an diesen nach unserer Spielregel erzeugten Zahlenfolge ist, dass sie Zahlen liefert, die mal größer mal kleiner sind, ohne dass eine Regel für das Auf und Ab gefunden werden könnte. Auch dass alle bekannten Folgen irgendwann auf die 1 stoßen wirkt überraschend. Für die Vermutungen, dieser Zahlenfolgen betreffend hat man bis heute noch keinen mathematischen Beweis gefunden. Man hat diesen Zahlenfolgen deshalb auch einen Namen gegeben. Sie heißen Ulam-Folgen. Was ist nahe liegender, als die Zahlen von Ulamfolge durch ein Programm errechnen zu lassen. Der eigentliche Algorithmus ist nicht sehr schwer: |
|
Man muss nur wissen, dass
i % 2
den Rest der Division von i durch
2
liefert. In den runden Klammern hinter dem Wort
if
wird also geprüft, ob der Rest bei der Division
0,
die Zahl i
also gerade ist. Der Ausdruck i =
i/2
dividiert den aktuellen Wert von
i durch
2
und speichert diesen neuen Wert wieder in der Variablen
i.
Entsprechendes gilt für i = i*3+1. Da wir davon ausgehen, dass die Folge über kurz oder lang bei der 1 landet und wir dann die Berechnungen abbrechen wollen, fügen wir unseren Quelltext in eine while-Schleife, deren Schleifenkörper solange immer wieder abgearbeitet wird, solange i nicht 1 ist:
|
|
|
Download: Ulam.java |
import turtle.*; |
| zu | 11.3 Chaosspiel |
| zur Startseite | www.pohlig.de (C) MPohlig 2004 |
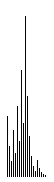 Nun sollten wir die
errechneten Zahlen unserer Ulamfolge auch grafisch darstellen. Wir wollen
dies so tun, dass eine Turtle schmale Balken (Striche) zeichnet, deren
Längen gerade die Zahlen darstellen.
Nun sollten wir die
errechneten Zahlen unserer Ulamfolge auch grafisch darstellen. Wir wollen
dies so tun, dass eine Turtle schmale Balken (Striche) zeichnet, deren
Längen gerade die Zahlen darstellen.