|
if - if - if |
Wir
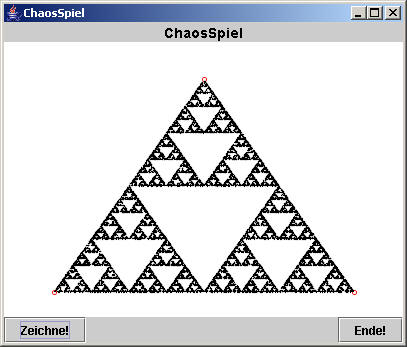
machen ein neues Spiel. Seine Regeln heißen.Markiere die Eckpunkte eines gleichseitigen
Dreiecks: P1, P2 und P3.
Wiederhole (‚sehr oft‘)
-
Wähle einen beliebigen Punkt auf dem Zeichenblatt.
-
Wähle P1, P2 oder P3 zufällig: Würfle und teile die
Augenzahl, wenn sie größer ist als 3 durch 2. Die so
gewonnene Zahl ist der Index des Punktes.
-
Gehe von der aktuellen Position um die halbe Distanz auf
den ‚gewürfelten Punkt‘ und markiere diesen Punkt.
Er ist die neue Position.
Am besten führe man den Algorithmus
zunächst einmal auf dem Papier aus, bevor wir ihn in Java implementieren.
|
Download:
Chaosspiel.java
|
import turtle.*;
import java.awt.*;
/**
* Turtle-Projekt: ChaosSpiel.java
* @version 1.0 vom 15.01.2004
* @author Michael Pohlig
*/
public class ChaosSpiel extends TurtleFrame {
//t1 wird deklariert
MeineTurtle t1;
// Festlegung der Koordinaten für das Dreieck
double xA = -150, yA = -50,
xB = 150, yB = -50,
xC = 0, yC = 150*Math.sqrt(2)-50;
//Die Start-Position der Turtle wird per Zufall gesetzt.
double xStart = Math.random()*400-200;
double yStart = Math.random()*400-200;
//In Zufall wird das Ergebnis des Würfelns gespeichert
int zufall;
//In schritt wird die Schrittlänge der Turtle gespeichert
double schritt;
public ChaosSpiel(String title) {
super(title);
//t1 wird erzeugt
t1 = new MeineTurtle(tWin);
//t1 erhält die Farbe rot
t1.setColor(Color.RED);
//t1 zeichnet die drei Eckpunkte des Dreiecks
t1.circle(xA,yA,2);
t1.circle(xB,yB,2);
t1.circle(xC,yC,2);
//Die Farbe für t1 wird auf schwarz zurückgesetzte
t1.setColor(Color.BLACK);
//Die Turtle nimmt die Startposition ein
t1.jumpTo(xStart,yStart);
}
public void zeichne() {
for(int i =0; i <100; i++){
//es wird ein Dreieckspunkt 'gewürfelt'
zufall = (int)(3*Math.random())+1;
if (zufall==1) {
//Der Abstand der Turtle zu dem gewürfelten
//Punkt wird berechnet und in der Variablen schritt
//gespeichert
schritt = Math.sqrt(Math.pow(xA-t1.getX(),2)
+Math.pow(yA-t1.getY(),2));
//t1 richtet sich in Richtung gefürfelten Eckpunkt aus
t1.turnTo(xA,yA);
//t1 nimmt den Zeichenstift hoch
t1.up();
//t1 bewegt sich auf Eckpunkt (halbe Entfernung) zu
//ohne zu zeichnen
t1.forward(0.5*schritt);
//t1 setzt den Zeichnstift wieder ab
t1.down();
//t1 markiert seine aktuelle Position mit einen
//kleinen Kreis.
t1.circle(t1.getX(),t1.getY(),0.1);
}
if (zufall==2) {
schritt = Math.sqrt(Math.pow(xB-t1.getX(),2)
+Math.pow(yB-t1.getY(),2));
t1.turnTo(xB,yB);
t1.up();
t1.forward(0.5*schritt);
t1.down();
t1.circle(t1.getX(),t1.getY(),0.1);
}
if (zufall==3) {
schritt = Math.sqrt(Math.pow(xC-t1.getX(),2)
+Math.pow(yC-t1.getY(),2));
t1.turnTo(xC,yC);
t1.up();
t1.forward(0.5*schritt);
t1.down();
t1.circle(t1.getX(),t1.getY(),0.1);
}
}
}
public static void main (String[] args) {
new ChaosSpiel("ChaosSpiel");
}
}
|
| |
Zeilenkommentare erläutern die einzelnen Anweisungen. Wir erkennen, dass
Java es erlaubt, auf die
else-Anweisung
zu verzichten, dann nämlich, wenn in ihrem Block nichts stehen würde.
In der zweiten und dritten
if-Anweisung
wurde auf die Kommentierung verzichtet, da die Anweisungen in allen drei
Blöcken sich nur in dem Namen des anvisierten Punktes unterscheiden.
Um vom Bediener des Programmes nicht
zu verlangen, dass er tausendfach den zeichne!-Schalter drückt, ist im
Programm zusätzlich eine
for-Schleife
eingebaut, die pro Klick auf den zeichne!-Schalter die Turtle veranlasst
100 Punkte zu setzen.
|
|
Bemerkungen
Download:
MeineTurtle. class |
Um die
drei Eckpunkte des Dreiecks und die Positionsmarkierungen der Turlte beim
Spiel zu zeichnen, benutzen wir, die selbst geschrieben Methode
circle(double
x, double y,
double radius) in
der Klasse MeineTurtle.
Aus diesem Grund ist t1 nicht mehr vom Typ
Turtle,
sondern vom Typ MeineTurtle,
die, wir erinnern uns, von Turlte
erbt (MeineTutle.class,
das Kompilat von MeineTurtle.java
muss sich also im gleichen Verzeichnis wie
Chaosspiel.java
befinden. |