|
12.4 Der ggT - Version 1 |
|
| Der ggT zweier natürlicher Zahlen a und b ist bekanntlich als diejenige größte (natürliche) Zahl definiert, die sowohl a als auch b ohne Rest teilt. | |
|
Download: GgT1.java
|
|
|
Das Programm ist leicht zu verstehen
und die Eingabe von Testzahlen liefert das gewünschte Ergebnis. Allerdings
dauert es recht lange, wenn wir für a und b größere Zahlen wählen, wie das
Beispiel a
= 162019746 und b = 115728390 zeigt.
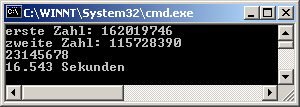
ggT(162019746, 115728390) = 23145678 Bis das Ergebnis auf dem Bildschirm erscheint vergehen einige Sekunden (Wie viel Sekunden tatsächlich vergehen, hängt natürlich vom Rechnertyp ab) . Das Ergebnis wurde mit dem CAS-System Mathematica(TM) überprüft. Wir wollen eine Klasse StoppUhr verwenden, um die Laufzeit unseres Algorithmus zu testen |
|
|
Download: StoppUhr.class |
Speichern Sie dazu die Klasse stoppUhr,class in das Verzeichnis, in dem auch das Programm GgT.java gespeichert ist. |
|
|
| Erläuterungen |
Zeile //1
zeigt wie eine Stoppuhr unserem Programm zugefügt wird. Was hier passiert, werden wir später genauer untersuchen, zur Syntax sei soviel gesagt: So wie wir eine Variable a vom Typ int deklarieren, nämlich int a; deklarieren wir eineStoppUhr als Objekt der Klasse StoppUhr mit: StoppUhr eineStoppUhr; Und so wie einer Deklaration von a eine Initialisierung folgt a = 5; folgt unter Zuhilfenahme des new-Operators und des Aufrufs eines sog. Konstruktors die Initialisierung, oder wie wir sagen lieber sagen, die Instanziierung des Objekts eineStoppUhr. eineStoppUhr = new StoppUhr(); Und schließlich: So wie man Deklaration und Initialisierung zusammenfassen kann zu int a = 5; so lassen sich Deklaration und Instanziierung eines StoppUhr-Objektes ebenfalls zusammenfassen: StoppUhr eineStoppUhr = new StoppUhr(); Zeile //2 und Zeile //3 Wie der Name verrät startet die Methode starten(), angewandt auf das Objekt eineStoppUhr dieses. Entsprechendes gilt für die Methode stoppen(). Zeile//4 Das StoppUhr-Objekt wird
ausgegeben, was so geschieht, dass die zwischen Starten und Stoppen
vergangene Zeit in Sekunden ausgegeben wird. |
| Ausgabe |
Natürlich hängt die
Laufzeit vom Rechner ab. Das gezeigte Ergebnis wurde auf einem Pentium III
450 MHz , 256 MB (Win2000) erzielt. |
|
Für Neugierige:
Download: StoppUhr.java |
Es ist klar, dass das Ergebnis sehr
unbefriedigend ist. Die Laufzeit des Algorithmus ist entschieden zu lang.
Der nach Euklid benannte Algorithmus stellt eine wesentlich schnellere
Variante dar. Ihm wenden wir uns im nächsten Kapitel zu. |
| zu | 12.5 Der ggT - erweiterter Euklidscher Algorithmus |
| zur Startseite | www.pohlig.de (C) MPohlig 2003 |