PrivateKey.
java

rsa(String originalText, String n, String e): String bzw

rsa(String geheimText, String n, String d): String

Die 'alten' Methoden sollten zu

rsa(String originalText, double n, double e): String bzw.

rsa(String geheimText, double n, double d): String

umgeschrieben werden. Ihr Methodenrumpf wird sehr einfach, wenn man die neuen Methoden (also die, die nur String-Objekte in den Parameterlisten besitzen) verwendet.

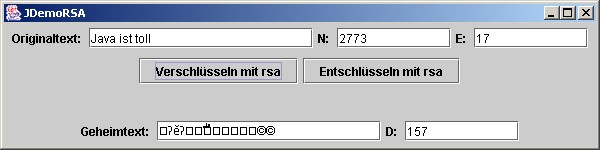
Schreiben Sie eine GUI JDemoRSA für die rasa(...)-Methoden in den Klassen EnKrypt und DeKrypt. Das Design ist durch das Bild unten vorgegeben.
 

public static String rsa(String originalText, String n, String e){

  //Das Ensemle (n,e) stellt den public key des RSA-Verfahrens dar

  String geheimText = "";

  java.math.BigInteger nBig = new java.math.BigInteger(n);

  java.math.BigInteger eBig = new java.math.BigInteger(e);

  java.math.BigInteger mBig;

  int c;



  for (int i = 0; i < originalText.length(); i++){

    mBig = new java.math.BigInteger(""+(int)originalText.charAt(i));

    c = mBig.modPow(eBig,nBig).intValue();

    geheimText += (char)c;

  }

  return geheimText;

}

public static String rsa(String originalText, long n, long e){

  return rsa(originalText, new Long(n).toString(), new Long(e).toString());

}

Die zweite rsa(...)-Methode ruft lediglich die erste rsa(...)-Methode auf. Das hat den Vorteil, dass Veränderungen (im Algorithmus nur einmal gemacht werden muss. Redundanzen und Fehler werden damit weitgehend vermieden. Eine Bemerkung noch zu

new Long(n).toString()

in der Parameterliste. Uns steht der Wert des einfachen Datentyps long zu Verfügung, etwa 17. Wir benötigen aber den String "17". Dazu müssen wir die Zahl 17, im allgemeinen also n als Objekt der Klasse Long erzeugen. Mit new Long(n) haben wir ein solches anonymes Objekt erzeugt (Das Objekt heißt anonym, da es keinen Bezeichner gibt, über den man auf das Objekt zugreifen könnte, was wir ja auch gar nicht wollen) . Schließlich rufen wir für dieses anonyme Objekt die Long - Methode toString() auf.

Die rsa(...)-Methoden in der Klasse DeKrypt sind entsprechend implementiert und werden deshalb hier nicht extra aufgeführt.
 

import java.awt.*;

import java.awt.event.*;

import javax.swing.*;



public class JDemoRSA extends JFrame implements ActionListener {

  // Anfang Variablen

  JButton rsaEnKryptButton, rsaDeKryptButton;

  JTextField eingabeFeldOT, eingabeFeldGT,

             eingabeFeldN, eingabeFeldE, eingabeFeldD ;

  JLabel labelOT, labelGT,

         labelN, labelE, labelD;



  JPanel norden, sueden, zentrum;

  // Ende Variablen



  public JDemoRSA (String title) {

    // Frame-Initialisierung

    super (title);

    setDefaultCloseOperation(EXIT_ON_CLOSE);



    Container cp = getContentPane();

    cp.setLayout(new BorderLayout());

    

    norden = new JPanel(new FlowLayout());

    cp.add(norden,BorderLayout.NORTH);



    sueden = new JPanel(new FlowLayout());

    cp.add(sueden,BorderLayout.SOUTH);



    zentrum = new JPanel(new FlowLayout());

    cp.add(zentrum,BorderLayout.CENTER);

    

    setSize(600, 150);





    // Anfang Komponenten

    rsaEnKryptButton = new JButton("Verschlüsseln mit rsa");

    rsaEnKryptButton.addActionListener(this);



    rsaDeKryptButton = new JButton("Entschlüsseln mit rsa");

    rsaDeKryptButton.addActionListener(this);

    

    eingabeFeldOT = new JTextField(20);

    eingabeFeldN = new JTextField(10);

    eingabeFeldD = new JTextField(10);

    eingabeFeldE = new JTextField(10);

    eingabeFeldGT = new JTextField(20);

    

    labelOT = new JLabel("Originaltext: ");

    labelN = new JLabel("N: ");

    labelE = new JLabel("E: ");

    labelD = new JLabel("D: ");

    labelGT = new JLabel("Geheimtext: ");

    

    norden.add(labelOT); norden.add(eingabeFeldOT);

    norden.add(labelN); norden.add(eingabeFeldN);

    norden.add(labelE); norden.add(eingabeFeldE);



    zentrum.add(rsaEnKryptButton);

    zentrum.add(rsaDeKryptButton);



    sueden.add(labelGT); sueden.add(eingabeFeldGT);

    sueden.add(labelD); sueden.add(eingabeFeldD);

    

    setVisible(true);

    // Ende Komponenten

  }



  // Anfang Ereignisprozeduren

  public void actionPerformed(ActionEvent ae) {

    Object obj = ae.getSource();



    if (obj == rsaEnKryptButton){

       String ot = eingabeFeldOT.getText();

       String n = eingabeFeldN.getText();

       String e = eingabeFeldE.getText();

       eingabeFeldGT.setText(EnKrypt.rsa(ot,n,e));

    }

    if (obj == rsaDeKryptButton){

       String gt = eingabeFeldGT.getText();

       String n = eingabeFeldN.getText();

       String d = eingabeFeldD.getText();

       eingabeFeldOT.setText(DeKrypt.rsa(gt,n,d));

    }

  }

  // Ende Ereignisprozeduren



  public static void main (String[] args) {

    new JDemoRSA("JDemoRSA");

  }

}