| 4.9.2 Four
Cool Cats |
|
| Noch eine kleine Übung |
In der MNU-Zeitschrift (Zeitschrift:
Der mathematisch naturwissenschaftliche Unterricht Jahrgang 56 2003 Heft
8) findet sich unter der Ruprik „Zu guter Letzt – alte und neue Fragen“
ein Aufgabe von F. K. Schmidt: Auf den Ecken eines Quadrats sitzt je eine Katze. Alle laufen gleichzeitig mit gleicher Geschwindigkeit los. Jede hält dabei direkt und permanent auf die links von ihr laufende Katze zu. Wo treffen die Tiere zusammen und welche Länge hat die Bewegungslinie? Den ersten Teil der Aufgabe können wir experimentell mit 4 Turtlen (die jetzt eben zu Katzen werden) beantworten. Finden Sie die Lösung? |
| Lösung | Da die
Katzen über die gleiche Funktionaliät verfügen wie sie unsere Turtle hat,
liegt es nahe, die Katzen als Objekte der Turtle zu erzeugen. Nenne wir
sie Mimi, Tiger, Morle und Pavarotti. Wie wir sie erzeugen, sie in einem
Quadrat aufstellen, zur besseren Unterscheidung eine Farbe geben und die
ihre Startposition mit ihrem Namen beschriften, steht im Konstruktor:public FourCoolCats(String title) {
super(title);
mimi = new Turtle(tWin);
mimi.jumpTo(-100,100); //Mimi sitzt links oben
mimi.setColor(Color.MAGENTA);
mimi.writeTo("Mimi",-120,110);
tiger = new Turtle(tWin);
tiger.jumpTo(100,100); //Tiger sitzt rechts oben
tiger.setColor(Color.RED);
tiger.writeTo("Tiger",80,110);
morle = new Turtle(tWin);
morle.jumpTo(100,-100); //Morle sitzt rechts unten
morle.setColor(Color.BLACK);
morle.writeTo("Morle",80,-120);
pavarotti = new Turtle(tWin);
pavarotti.jumpTo(-100,-100); //pavarotti links unten
pavarotti.setColor(Color.BLUE);
pavarotti.writeTo("Pavarotti",-120,-120);
//Damit sind die Katzen im Uhrzeigersinn aufgestellt.
// Mimi Tiger
// pavarotti Morle
}
|
|
Download: FourCoolCats. java |
public void zeichne() {
mimi.turnTo(tiger.getX(),tiger.getY());
mimi.forward(1);
tiger.turnTo(morle.getX(),morle.getY());
tiger.forward(1);
morle.turnTo(pavarotti.getX(),pavarotti.getY());
morle.forward(1);
pavarotti.turnTo(mimi.getX(),mimi.getY());
pavarotti.forward(1);
}
Wir müssen 200 mal auf den
Zeichne! - Schalter klicken um den ganzen Weg
while(
mimi.getX() != 0 || mimi.getY() != 0){ Tatsächlich führt dies
zu einer Endlosschleife. Um das einzusehen schauen
wir uns den Gang der 4 Katzen an, wenn
|
| Bemerkung | Das Mathematische Modell zur Aufgabe liefert vier Wege für die Katzen, die aus unendlich vielen Schritten besteht. Trotzdem konvergieren sie (treffen sich) und die Gesamtlänge hat einen endlichen Wert. Das Paradoxon ist vergleichbar mit dem Rennen zwischen Achilles und der Schildkröte |
| zu | 4.10 Verzweigung |
| zur Startseite | www.pohlig.de (C) MPohlig 2004 |
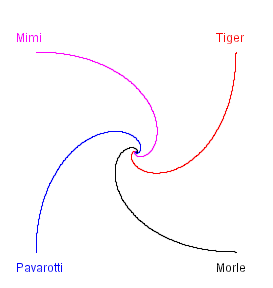 der
4 Katzen zu bekommen: Natürlich hätten wir gerne, dass wir die ganze
Darstellung bekommen, ohne dass wir wiederholt den Zeichne! - Schalter
drücken. Wir brauchen dazu die 8 Zeilen in der
zeichne()-Methode
mur in den Rumpf einer Schleife zu schreiben. Wir können eine
for-Schleife
mit 200-Durchgängen benutzen oder eine
while-Schleife.
Eine Abbruchbedingung ist in diesem Fall etwas schwer zu finden. Aus
Symmetriegründen können wir, schon bevor wir die Zeichnung uns ansehen
sagen: Wenn sich die Katzen treffen, dann im Ursprung (0/0). Als
Abbruchbedingung hätten wir dann die Forderung, dass
mimi.getX() == 0 && mimi.getY() == 0 Oder
anders
der
4 Katzen zu bekommen: Natürlich hätten wir gerne, dass wir die ganze
Darstellung bekommen, ohne dass wir wiederholt den Zeichne! - Schalter
drücken. Wir brauchen dazu die 8 Zeilen in der
zeichne()-Methode
mur in den Rumpf einer Schleife zu schreiben. Wir können eine
for-Schleife
mit 200-Durchgängen benutzen oder eine
while-Schleife.
Eine Abbruchbedingung ist in diesem Fall etwas schwer zu finden. Aus
Symmetriegründen können wir, schon bevor wir die Zeichnung uns ansehen
sagen: Wenn sich die Katzen treffen, dann im Ursprung (0/0). Als
Abbruchbedingung hätten wir dann die Forderung, dass
mimi.getX() == 0 && mimi.getY() == 0 Oder
anders 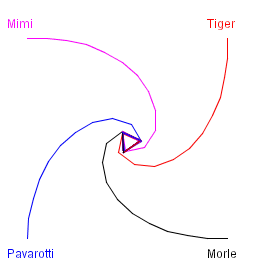 wir
als Schrittweite 20 wählen würden: Wie das Bild zeigt, ist der Gang der
Katzen nicht exakt so, wie er in der Aufgabe gefordert ist. Die Wege sind
nicht 'schön glatt' gekrümmt, sondern kantige Streckenzüge. Das führt
dazu, dass die 4 Katzen um den Ursprung wie um den heißen Brei 'tanzen'.
Die Abbruchbedingung, wie wir sie in der
while
- Schleife gefordert haben, wird also nie erreicht. Auch wenn wir eine
Schrittweite 1 wählen, wie unserem Beispiel, passiert das gleiche, nur
reicht die Auflösung des Bildschirms nicht aus um dies zu erkennen. Also
wird auch hier die Abbruchbedingung nie erreicht, wir müssen deshalb die
x- und y- Koordinaten der Position von Mimi bei der Abfrage runden. Die
ganze zeichne()
- Methode hat damit die Gestalt:
wir
als Schrittweite 20 wählen würden: Wie das Bild zeigt, ist der Gang der
Katzen nicht exakt so, wie er in der Aufgabe gefordert ist. Die Wege sind
nicht 'schön glatt' gekrümmt, sondern kantige Streckenzüge. Das führt
dazu, dass die 4 Katzen um den Ursprung wie um den heißen Brei 'tanzen'.
Die Abbruchbedingung, wie wir sie in der
while
- Schleife gefordert haben, wird also nie erreicht. Auch wenn wir eine
Schrittweite 1 wählen, wie unserem Beispiel, passiert das gleiche, nur
reicht die Auflösung des Bildschirms nicht aus um dies zu erkennen. Also
wird auch hier die Abbruchbedingung nie erreicht, wir müssen deshalb die
x- und y- Koordinaten der Position von Mimi bei der Abfrage runden. Die
ganze zeichne()
- Methode hat damit die Gestalt: