|
14 Rekursive Grafiken 14.1 Binärer Baum |
|
|
Download: EinT.java |
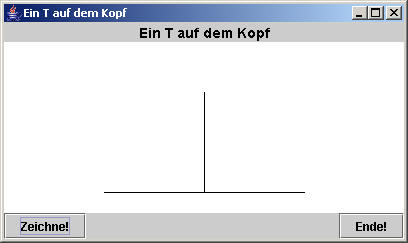
Bevor wir
uns mit einem sog. Binärbaum beschäftigen, zeichnen wir mit der
Turtle ein T, das auf dem Kopf steht.
Die Methode zeichne() in unserer Turtlevorlage ist sehr einfach: public void zeichne() {
t1.jumpTo(0,150);
t1.forward(-100);
t1.right(90);
t1.forward(100);
t1.forward(-200);
}
|
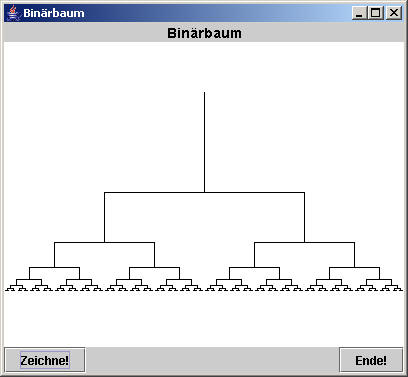
| Aus dem auf dem Kopf stehenden T bekommen wir einen Binärbaum, wenn wir an die Enden des Balkens wieder auf dem Kopf stehende Ts, allerdings jetzt kleiner, ansetzen und dieses Vorgehen immer weiter wiederholen. Wir erhalten: | |
|
|
|
Die
entstandene Figur zeigt eine interessante Eigenschaft: Wählen wir aus dem
Bild geschickt einen Teilbereich heraus und zoomen ihn größer, so entsteht
eine Figur, die von der ganzen nicht zu unterscheiden ist. Wir können auch
sagen, in einer Teilfigur steckt die ganze Information für die
Gesamtfigur. Solche Figuren nennt der Mathematiker selbstähnlich. Wie aber
programmieren wir einen solchen Baum? Eine Methode zeichne() mit der
folgenden Gestalt würde uns gefallen: public void zeichne() {
double l = 100;
t1.jumpTo(0,150);
t1.zeichneBinaerBaum(l);
}
|
|
| API-der Turtle | In einer
Variable l
legen wir die Länge der Teilstrecken des ersten Ts fest und zeichnen den
Binärbaum, in dem wir die Methode
zeichneBinaerBaum(
double l) für
unser Turtle-Objekt t1
aufrufen. Aber halt! Wie ein Blick in die API-der Klasse
Turtle
zeigt, gibt es diese Methode in der Klasse Turtle nicht. Also müssen wir
sie selbst implementieren. Das ist aber nicht so einfach, denn die Turtle
ist in einem Paket und ihr Quelltext ist uns nicht zugänglich. Uns bleibt
nur der Weg, den wir schon einmal in
10.1
Die Klasse MeineTurtle erbt von Turtle gegangen sind: Wir schreiben
uns eine Klasse, die von der Klasse
Turtle
erbt und in die wir unsere Methoden für grafische Rekursionen unterbringen
wollen. Wir nennen diese Klasse deshalb:
RekursionsTurtle. |
import turtle.*;
public class RekursionsTurtle extends Turtle{
public RekursionsTurtle(TurtleWindow tWin){
super(tWin);
}
public void zeichneBinaerBaum(double l){
if (l>1){
forward(-l);
right(90); forward(l); left(90);
zeichneBinaerBaum(l/2);
right(90); forward(-2*l); left(90);
zeichneBinaerBaum(l/2);
right(90); forward(l); left(90); forward(l);
}
}
}
|
|
|
Download: RekursionsTurtle. class Binaerbaum.java |
Uns
wundert nicht, dass wir unsere Methode, wegen der Selbstähnlichkeit
rekursiv aufbauen: Wie der rekursive Aufruf zeigt, wird bei jedem Schritt tiefer in die Rekursion, die Länge der T-Strecken halbiert. Den Basisfall haben wir erreicht, wenn die Länge (sie ist eine Fließkommazahl) kleiner als 1 wird. Vergleichen wir unsere Methode mit der zeichne()-Methode in EinT: Wir sehen zunächst die gleichen Turtle-Methode, sie sind gelb unterlegt. Statt der festen Schrittlänge 100 haben wir allerdings die Schrittlänge l. An den Enden des T-Querbalkens setzen wir die kleineren Ts an in dem wir die Methode zeichneBinaerBaum(double l) mit halber Schrittlänge rekursiv aufrufen. Die rekursiven Aufrufe sind grün unterlegt. Vor dem rekursiven Aufruf muss unsere Turtle aber in die richtige Richtung für das T-zeichnen ausgerichtet und nach dem rekursiven Aufruf wieder in die richtige 'Wanderrichtung' zurückgesetzt werden. Deshalb die Aufrufe left(90) vor und right(90) nach dem rekursiven Aufruf (blau unterlegt). Schließlich muss die Turtle in ihren Ausgangspunkt zurückgeführt werden: forward(l); left(90); forward(l) (weiß unterlegt). Um sich klar zu machen, warum im Gegensatz zum Zeichnen des einfachen Ts dieses Rückführen wichtig ist, lassen man diese drei Anweisungen einfach mal weg. |
| Bemerkung zum Testprogramm |
import turtle.*;
import java.awt.*;
/**
* Turtle-Projekt: Binaerbaum.java
* @version 1.0 vom 14.12.2003
* @author Michael Pohlig
*/
public class Binaerbaum extends TurtleFrame {
RekursionsTurtle t1;
public Binaerbaum(String title) {
super(title);
t1 = new RekursionsTurtle(tWin);
}
public void zeichne() {
double l = 100;
t1.jumpTo(0,150);
t1.zeichneBinaerBaum(l);
}
public static void main (String[] args) {
new Binaerbaum("Binärbaum");
}
}
|
|
Damit
t1
über die neue Methode
zeichneBinaerBaum(double l)
verfügt muss sie ein
RekursionsTurtle-Objekt sein.
Der neue Konstruktor muss angepasst werden: Über
super(titel)
rufen wir den alten Konstruktor von Turtle auf, so ist gewährleistet, dass
unser Binaerbaum-Objekt
auch über die Funktionalität der Klasse
TurtleFrame
verfügt. |
|
| zu | 14.2 Sierpinski-Dreieck (Version 2) |
| zur Startseite | www.pohlig.de (C) MPohlig 2004 |